A while back, in 2018, I had a flash of inspiration to try combining a bunch of tilted rings into the shape of a torus. The goal was to render something akin to a Spiral Torus. A few hours later, I produced this:
See the Pen
inner torus by Ryan Thavi (@rthavi)
on CodePen.
After experimenting with some colors, lights, and noise, I published it, and it hasn’t changed much since! I intentionally kept it very minimal with no configuration or parameters, which I believe has contributed greatly to its popularity. It’s actually one of my most popular creations to date, and even I still find myself coming back to watch it. In this series of posts, I’m going to revisit this concept in sections and rebuild it step-by-step, but with some enhanced features like a UI and a refactored codebase.
This article is intended for someone who has at least a beginner’s knowledge of HTML5 and JavaScript. If you are unfamiliar with the fundamentals, my CodePen examples will make it very easy for you to dive in and start coding without having to worry about setting up a development environment, but you will probably have a lot of questions that won’t be addressed. W3 Schools and the Mozilla Developer Network are fantastic resources that I still return to as a seasoned developer. Googling is always an option, particularly for one-off bugs, but references like these tend to broaden your understanding and expose you to other language features rather than just solve a single problem.
Original Concept
Let’s begin with a “Hello World” of this concept. The basic Inner Torus concept was a torus composed of many, much smaller torii that were positioned and angled strategically. My first pass would therefore be just to render multiple torii on the screen at once. There are multiple approaches, so let’s step through my own strategy with some examples. I’m using the Processing library for Javascript, p5.js. If you’ve never used this library, it’s about as straightforward as it gets to start making graphics with code. You declare setup and draw functions, and then the Processing engine takes over when the page loads.
Let’s declare these two methods, fill them in with some boilerplate, and render a bunch of torii. I’m also going to make the whole rendering rotate so we can get a look at it from multiple angles.
function setup() {
createCanvas(window.innerWidth, window.innerHeight, WEBGL); // creates new canvas of given size, sets up 3D rendering
camera(0, 0, 800, 0, 0, 0, 0, 1, 0); // puts camera out 800 units away from origin along z-axis. Sets Y-axis as vertical
}
function draw() {
background(0); // clears previous frame
orbitControl(); // allows user to control camera with mouse
rotateY(frameCount * 0.003); // rotates the *entire* space proportional to elapsed time
for (let i = 0; i < 5; i++)
{
push(); // push a new transformation state onto the stack
translate(0, 0, i * 25); // perform transformation (translate in the z direction)
torus(50, 6); // render the torus
pop(); // pop off current transformation state
}
}
To break down setup, which is only invoked once, during initialization:
- Tell p5.js to render an HTML5 canvas the size of the window and pass in WEBGL as an argument. WEBGL isn’t a string, it’s a constant from p5.js which tells the engine that it will be rendering this drawing in 3D.
- Set the camera out 800 units in the Z-axis. That points towards the screen. We also set the camera to orient itself such that the (negative) Y-axis points upward. For more on the default coordinate system, check out this reference page.
Similarly, for draw, which is called once per frame:
- Clear the whole frame out and set it to black.
- Turn on orbitControl, which allows the user to manipulate the camera with their mouse.
- Rotate the entire space around the Y-axis proportional to the amount of time the drawing has been running. I like to calculate this based on the frameCount.
- Render 5 rings. Between each call to the torus function, which simply draws a torus on the screen, we push/pop and translate in between. We’re going to take a deeper look at this concept, as it is a useful strategy to keep in mind.
One final thing to note is that when torus is called, Processing renders the torus such that the ring radius rotates around the z-axis, thus it radiates outward on the plane composed of the x and y axes. It’s also a good time to point out that the torus function takes two parameters, which on Wolfram Alpha, are called the c and a axes. In Processing, they’re called the radius and tube radius.
Push/Pop, the Stack, and transformations
If push and pop don’t make you think of the data structure known as a stack, then allow me to provide some background. A stack is a simple data structure where we think of pushing items onto the top of the stack and popping items off of the top of the stack. We like this idea conceptually because it is simple to work with and can serve as the data structure for algorithms (and there are a lot of them) that require the most recent item added to the stack to be processed first. In other words, a stack has Last In, First Out (LIFO) behavior. Don’t get too sidetracked here, it won’t take long for it to click once you start coding.
We will be applying this strategy to accumulate instructions that need to go to the rendering engine in a specific order. Certain commands to the Processing engine change the current origin (where x = 0, y = 0, and z = 0) of the drawing, as well as any angular orientation. Remember earlier we said that the positive y-axis was up? This is why we also tell the drawing to rotate around the y-axis.
Instead of saying that you want to draw a dot at a point with coordinates (x,y), you instead move the origin to coordinates (x,y) and draw a dot at the origin. We generally call such instructions transformations, and they form the basis of many ideas in computer graphics. In Processing, these accumulate over the scope of a single draw, unless you enclose them in a set of push/pop calls. When we enclose transformations like this, we also un-apply them after we call pop. In this way, if you wanted to draw multiple dots, you would reset the origin each time you drew a dot.
for (let x = 0; x < 5; x++) {
for (let y = 0; y < 5; y++) {
push();
translate(x * 10, y * 10);
point(0, 0);
pop();
}
}
Conversely, you might not want to reset the origin each time. Going back to our torii, we could simply allow the translations to accumulate, moving the origin further along each time. Instead of scaling each translate call to i * 25, we just keep on translating by 25. After draw completes, all transformations are reset, so we’re done here. Simple!
function setup() {
createCanvas(window.innerWidth, window.innerHeight, WEBGL);
camera(0, 0, 800, 0, 0, 0, 0, 1, 0);
}
function draw() {
background(0);
orbitControl();
rotateY(frameCount * 0.003);
for (let i = 0; i < 5; i++)
{
translate(0, 0, 25); // notice there's no push or pop around this! We also no longer multiply by i
torus(50, 6);
}
}
We move the origin each time we call translate, so by the end of the loop we’re out 5 * 25 = 125 units from the origin along the Z axis. To make it explicitly clear, here’s a table that shows the transformed origin after each iteration:
| i | Origin |
|---|---|
| 0 | (0, 0, 25) |
| 1 | (0, 0, 50) |
| 2 | (0, 0, 75) |
| 3 | (0, 0, 100) |
| 4 | (0, 0, 125) |
In the following snippet, I’m going to use both strategies to render a stack. Notice that one stack renders further forward than the other. That’s because when we use push/pop, we initially scale by i * 25, where i === 0, and therefore the entire expression evaluates to 0. In the second loop, we accumulate translations of 25 starting at 25. There’s no right or wrong here, it’s situational and preferential! I’m going to prefer push/pop in this article because I want to add a lot of complexity to the work, and this is one of the simplest ways to encapsulate said complexity.
Creating the Big Torus
We have everything we need to get a rough sketch, we just need to play with the shape, orientation, and number of rings. Let’s start by just drawing all the rings together at the origin and rotating each one individually. We should end up with a sphere of rings. From here on out, I’ll limit my code snippets to only the relative subject matter:
for (let i = 0; i < 5; i++) {
push();
rotateY((i/5) * TAU);
torus(50, 6);
pop();
}
Notice that our transformation no longer places our rings in a linear stack, but they are instead rotated around the same vertical axis. Since we have called no translate function so far, our origin should still be at (0,0,0). What about this business with (i/5) * TAU? In general, tau is a mathematical symbol that has a value of 2 * pi. In Processing, it’s a pre-defined constant ready for you to use. There are a handful of others at your disposal as well. So all we’re doing is rotating by fractions of an entire 360° rotation! Let’s break it down:
| i | i / 5 | i/5 * TAU |
|---|---|---|
| 0 | 0 | 0° |
| 1 | 1/5 | 72° |
| 2 | 2/5 | 144° |
| 3 | 3/5 | 216° |
| 4 | 4/5 | 288° |
Notice we don’t actually calculate 360° in our code. That’s because 5/5 * TAU= 360°, which is equivalent to 0°. I find it cleaner to just start a rotational series at 0° since iteration indices almost always start at 0. It’s also worth noting that in its default configuration, Processing works with radians and not degrees, I’m only expressing these values in degrees here for ease of understanding.
Alright–so we can spin a bunch of torii. How do we start to spread them out? We already know that each torus radially lies along the x/y plane, so we should be able to translate outward along the x-axis (either positively or negatively) to spread out the torii around the y-axis.
We can also do this around the x or z-axes. I’ll demonstrate this concept for the x-axis in the next CodePen sample, but see if you can work it out yourself for revolution around the z-axis. It’s tricky!
See the Pen
inner torus post sample 2 by Ryan Thavi (@rthavi)
on CodePen.
for (let i = 0; i < 5; i++) {
push();
rotateY((i/5) * TAU);
torus(50, 6);
pop();
}
Refactoring
At this point, I’ve seen enough to know that I’m on the right track. As mentioned earlier, I intentionally kept the original code minimal. This time around, I’m going to get rid of all hardcoded values. I also know that I’m going to be using a specific library to create my UI, so I will be adhering to its convention for holding my configuration parameters. But first, let’s take this concept of drawing a torus from smaller torii and encapsulate that into its own object template, called a class. This concept of cleaning up the code to make it more configurable, modular, readable, and usable is called refactoring. My personal touchstone for a good refactor is readability.
There’s a famous programmer joke about how one of the hardest parts of programming is simply naming things. Yes. There is nothing more frustrating than looking at someone else’s (or more likely, my own) already arcane script and being unable to reason about single-letter variables like “a, b, c, d,…” which aren’t named according to their usage. You should be able to read the code in one pass and come away with a high-level idea of how it works. There are times it makes sense to use single-letter variables, and there might be some magical numeric operations in there that are unwieldy, but that’s why we have comments. Anyway, let’s get to it.
MetaTorus Class
Since we’re making a big torus of smaller torii, I’m going to call our construction a MetaTorus. I also want to preserve Processing’s own convention that we revolve the tube of the torus around the z-axis, which is, incidentally, the problem I asked you to solve on your own earlier!
push();
rotateY(HALF_PI);
for (let i = 0; i < 15; i++) {
push();
rotateX((i/15 * TAU);
translate(0, 100, 0);
torus(50, 6);
pop();
}
pop();
The trick to this lies in understanding how rotations of the default torus vary from one another. Rotating a torus around the z-axis is like turning a steering wheel–the ring is still in the same place. Rotating around the x or y-axes is more like spinning a quarter, which is why we can just translate outward laterally and visually create a larger torus. If you were to hold an arm straight out to your side holding out a ring and spin around, the path the ring takes would trace out a torus.
In order to do this about the z-axis, we must first rotate each torus by 90° around the y-axis. Can you see why we use y and not x? Also note that I chose to apply this transformation a single time, outside the loop. I know I need this single transformation to apply to all the torii, so why not do it once and be done with it? Semantically, the intention here is more clear than if I had chosen to rotate each torus individually. Finally, this is more performant. We’re doing it once instead of n = 15 times. This is probably an easy choice for everyone to make, but I like to stop and justify decisions like this frequently. It helps to produce much higher-quality code and results!
I initially drop the basic code into a class like this and simply verify all the pieces connect:
class MetaTorus {
constructor() {
}
render() {
push();
rotateY(HALF_PI);
for (let i = 0; i < 15; i++) {
push();
rotateX((i/15) * TAU);
translate(0, 100, 0);
torus(50, 6);
pop();
}
pop();
}
}
The rest of the code is updated to create a global metaTorus object, instantiate it during the setup call, and finally invoke the object’s render method within the draw function:
let metaTorus;
function setup() {
createCanvas(window.innerWidth, window.innerHeight, WEBGL);
camera(0, -200, 500, 0, 0, 0, 0, 1, 0);
metaTorus = new MetaTorus();
}
function draw() {
background(0);
orbitControl();
// rotate entire drawing
rotateY(frameCount * 0.003);
metaTorus.render();
}
…and now we need to work through what parameters we need in the constructor. Let’s take inventory of everything in the class so far:
- Total number of torii. We can think of this as the “resolution” of the MetaTorus. “n” is also an option here, since most people understand that to be the size of a collection. We could also be very direct and call it something like “numberOfRings“. For now, I’m going to settle on resolution, but I might rename it if it doesn’t read clearly.
- Radius of the MetaTorus. This is how far we translate out before rendering each subtorus. Our variable name should probably include the term “radius“, but there are other radii to consider. Let’s keep going.
- Tube Radius of the MetaTorus. This is trickier than it might initially seem. The “50” that we pass into each torus call in our prototype is actually the radius of each SubTorus, which only extends to the center of its own tube. So, this is technically the radius + tubeRadius of a SubTorus.
- Radius of a SubTorus. In the code above, this is our 50.
- Tube Radius of a SubTorus. In the code above, this is our 6.
A picture is worth a thousand words:
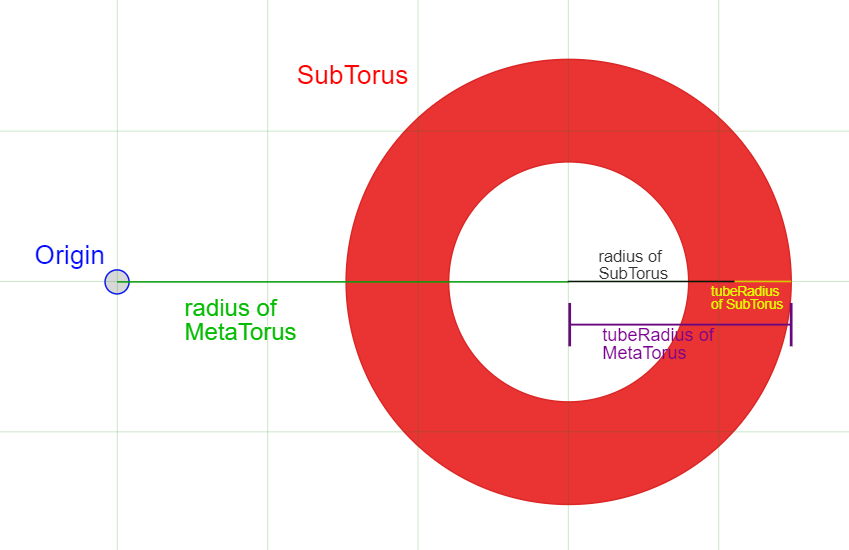
We want a ton of additional parameters as well, but let’s first tackle the immediate problem of refactoring these 5 values. If it’s not obvious yet–we actually only need 4 of them, since the tube radius of the larger MetaTorus is a function of the radii in the smaller SubTorii. We won’t bother to define it for now. I’ve settled on “main” and “sub” to differentiate between radii for the larger torus and its substituents, respectively.
class MetaTorus {
constructor(resolution, mainRadius, subRadius, subTubeRadius) {
this.resolution = resolution;
this.mainRadius = mainRadius;
this.subRadius = subRadius;
this.subTubeRadius = subTubeRadius;
}
render() {
push();
rotateY(HALF_PI);
for (let i = 0; i < this.resolution; i++) {
push();
rotateX((i/this.resolution) * TAU);
translate(0, this.mainRadius, 0);
torus(this.subRadius, this.subTubeRadius);
pop();
}
pop();
}
}
...
metaTorus = new MetaTorus(15, 100, 50, 6);
We’ll complete the refactor by moving all these hardcoded numbers into a global object, config, where we’ll name each property in good ol’ Javascript Object syntax (I’m going to change some values as well in order to make the MetaTorus more pleasant to look at):
let config = {
cam: {
x: 0,
y: -200,
z: 500,
centerX: 0,
centerY: 0,
centerZ: 0,
upX: 0,
upY: 1,
upZ: 0
},
mainRadius: 200,
resolution: 25,
rotationFrameScaling: 0.003,
subRadius: 75,
subTubeRadius: 10
};
...
camera(config.cam.x, config.cam.y, config.cam.z, config.cam.centerX, config.cam.centerY, config.cam.centerZ, config.cam.upX, config.cam.upY, config.cam.upZ);
metaTorus = new MetaTorus(config.resolution, config.mainRadius, config.subRadius, config.subTubeRadius);
...
rotateY(frameCount * config.rotationFrameScaling);
Wow, isn’t that a million times easier to reason about than soulless numbers in a function? camera alone has 9 arguments, but arranged like this it’s not so daunting anymore. In an upcoming step, we’ll install a rudimentary UI that will allow you to change all of these parameters during runtime and avoid having to re-type your code, refresh the page, etc.
If you’ve done everything correctly, your code should look something like this:
See the Pen
inner torus post sample 3 by Ryan Thavi (@rthavi)
on CodePen.
Wrapping Up Part 1
We’ve done quite a bit of work here, let’s take a break. In Part 2, we’ll add a UI, start tilting the rings, and finally add some style to it!
